From Marsh to Eleveld

In previous blogs, we promised to discuss changing models in your TCI devices and their clinical consequences. Having covered the transition 'From Schnider to Eleveld,' it's now time to explore the topic from a different starting point: the Marsh model.

Some time has passed since the last blog. The main reason for this delay is the recent focus on another very interesting drug: Ciprofol (or Cipepofol). Ciprofol is a GABA receptor agonist like propofol that offers the benefits of propofol but with fewer disadvantages, such as pain on injection and hemodynamic instability.

Ciprofol presents a potential replacement for good old propofol and possibly even remimazolam and is certainly an opportunity for implementation in Target Controlled Infusion (TCI). Hopefully, the multi-model mess that currently affects the acceptance of TCI technology by confusing users can be avoided. Stay tuned.

Like the Schnider model, the Marsh model comes in two versions. And, also similar to the Schnider model, the difference is the implementation of the blood-brain equilibration constant: keo, or when expressed as a half-life of this equilibration process: the thalfkeo. The difference with the implementation of the Schnider model in the open TCI devices, however, is that at least they are named differently: the Marsh model and the Modified Marsh model. But, similar to the confusion with the Schnider model, this confusion is partly caused by the adoption of the time-to-peak effect (TPE) concept based on bolus pharmacokinetics. Bolus pharmacokinetics simply do not fit in the infusion pharmacokinetics of a TCI system. In Tivatrainer, the Modified Marsh is called Marsh (larger keo), which already points to the differences. A 'larger' keo, or short thalfkeo, points to a fast equilibration of blood and brain concentration, and hence, the overshoot of the blood concentration in the effect-site control mode of TCI is small. In the original Marsh model, this blood-brain equilibration is slower and based on Auditory Evoked Potential (AEP)[2]. In contrast, the Modified Marsh is based on the TPE according to the BIS index. Like the Canonical Univariate Parameter of the processed EEG, used in the Schnider modeling of the pharmacodynamics, the AEP and the BIS are surrogate effect parameters that may, or may not, directly represent clinical endpoints like loss of consciousness (LOC). 

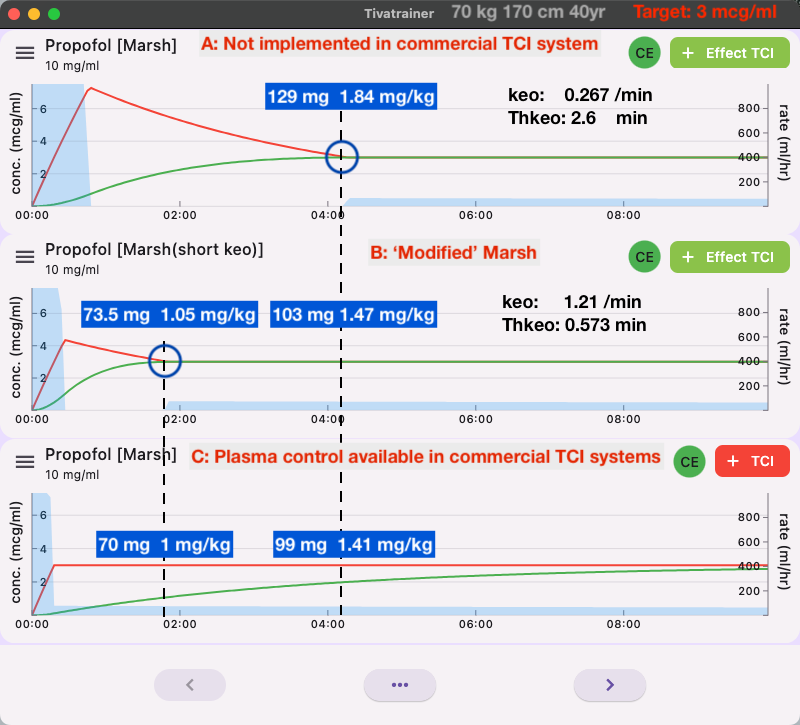
The dose given by effect-site control for a maintenance target with the Modified Marsh model is not likely to render unconciousness in all patients. Therefore, common practice, as with the Schnider model, is to start with a higher target and then decrease to the maintenance target. The small difference between the effect-site control with modified Marsh and plasma control in simulation C does, in our opinion, not justify this 'Modified' implementation of the Marsh model. It is another example of how uncritical implementation of an untested and unverified assumption further confuses the employability of TCI. One could even argue that plasma control is more optimal because, in effect-site control, a major dose is given at the beginning of induction, after which the pump stops for quite a while. In cases where fast distribution and clearance in the patient deviate considerably from the programmed parameters in the TCI device, it is theoretically possible that the patient will lose consciousness following the large initial dose and then wake up during the stopping period of the pump. In plasma control, the pump will keep running, and although the observed level may not match the targeted one due to non-matching pharmacokinetics, abrupt changes in the patient's status are avoided.

Why is effect-site TCI for the Marsh model not available when the induction dose is within the limits of the drug prescription advice (SPC) when given manually as a bolus (1.5-2.5 mg/kg)? First of all, the pharmacodynamic data were not available when the Diprifusor with the Marsh model was launched. Secondly, the 'short' keo was perceived as having too long a blood-brain equilibration time, as suggested in a clinical study [3]. Lastly, it became clear that the value of the keo was highly dependent on the type of surrogate effect measurement and even the measurement device itself that was used for the construction of the pharmacodynamic model [4]. For the Marsh model, an experimental auditory evoked potential(AEP) device was used, which essentially explained the hysteresis between drug concentration and drug effect, and this was used for the estimation of the keo. Later, other methods of estimating the keo were based on and tested against clinical endpoints, which pointed to an intermediate keo for the Marsh model [6][7][8]. Unlike the keo derived from surrogate effect measurements like BIS, CUP, AEP, etc., which use techniques like TPE and hysteresis curves, there is little difference in the keo based on clinical endpoints. However, this keo has never been implemented in commercially available TCI devices.

How does the Marsh model behave when the produced dose is resimulated in the Eleveld pharmacokinetic domain? Unfortunately, the Eleveld model also comes in two variants: with or without opioids. The Eleveld model without opioids is almost identical to the Marsh model for the average patient. The Eleveld model with opioids predicts an overall slightly higher concentration with the same dose due to the influence of the opioid on the pharmacokinetic properties of propofol. Primarily, the central clearance is lower. Even after several hours, the difference remains mainly an offset or bias around 15%, and this does not change over time. This possibly reflects the influence of the opioid on blood flow and drug transportation in the body.

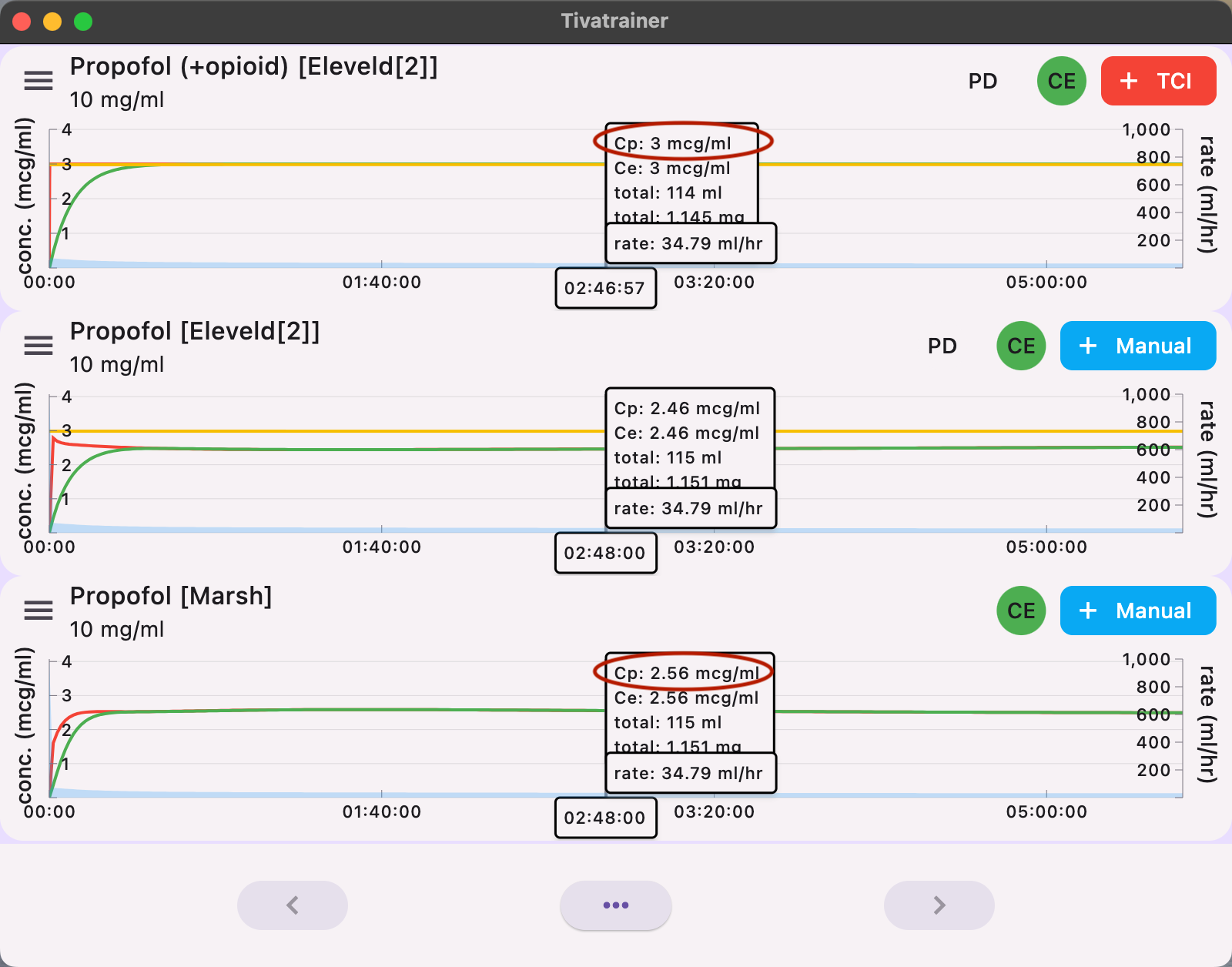
Changing from Marsh to Elevel: Is it necessary?

Our answer is yes for several reasons. Maybe not for the 'average' 70 kg, 40-year-old, 170 cm patient. The Eleveld model with opioids will simply administer about 15% less drug than the Marsh model for equivalent targets. This offset is constant and, hence, easily adjustable. However, for non-standard patients, things become more complicated :
- Elderly, frail patients need less, but how much less?
- It takes longer for the effect to occur in elderly patients, but how much longer?
- Obese patients need more, but how much more?
- Children.... well, they simply need another model, but which model and target? By incorporating anthropometric parameters, the Eleveld model offers more for TCI than the standard weight-related pharmacokinetic (Pk) model, like the Marsh model (and many other weight-based dosing schemes we use). The Eleveld model provides pharmacokinetic adaptations for a wide range of patients, from skinny to obese, young to old, male and female, based on scientific data. Anaesthesiologists are still left with the usual biological variability and clinical circumstances, which we know how to manage. On top of the pharmacokinetic adjustments for individual patients, the Eleveld model also predicts an age-adjusted concentration where 50% of the patients are above or below a BIS of 47. However, the Ce50 in the Eleveld model is not the effect level where 50% of the patients are expected to be asleep (LOC). The Ce50 for LOC is reported in many publications to occur around a BIS of 63 [5], at an effect-site concentration that is about 30% lower than the Ce50 in the Eleveld model. This Ce50 is represented by the yellow line in Tivatrainer and is not (yet) adjustable. In the previous blog, "From Schnider to Eleveld", we explained how you can retrieve this information on LOC using Tivatrainer. The relationship between the reduction in effect-site concentration, induction dose, increase in induction time, and age is complex but automatically handled by the Effect-TCI system contained in the Eleveld model.

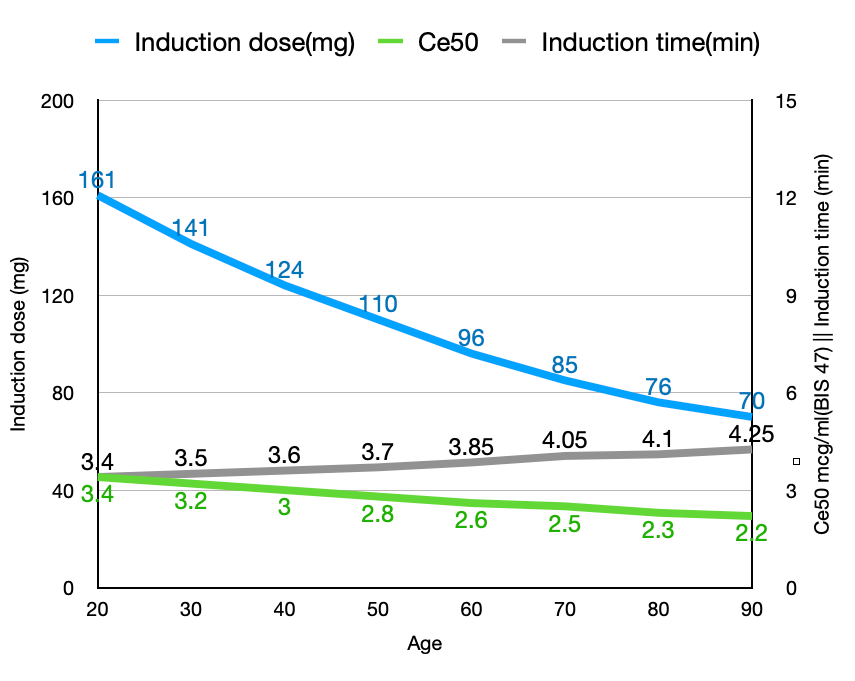
To achieve an effect-site concentration corresponding to the patient's age that correlates with a BIS of 47, the induction dose decreases from 161 to 70mg (a 57% reduction), the required Ce decreases from 3.4 to 2.2 mcg/ml (a 35% reduction), while the induction time increases from 3.4 to 4.25 minutes (a 25% increase). Note that the large decrease in the induction dose (161 mg to 70mg, or 2.3mg/kg to 1mg/kg) is the result of both age-related increased sensitivity and altered pharmacokinetics. 

If you do not have the Eleveld model available, you can use the IVAssist function of Tivatrainer to obtain an adjustable manual scheme that implements all the dependencies (age, weight, etc.) of the Eleveld model.

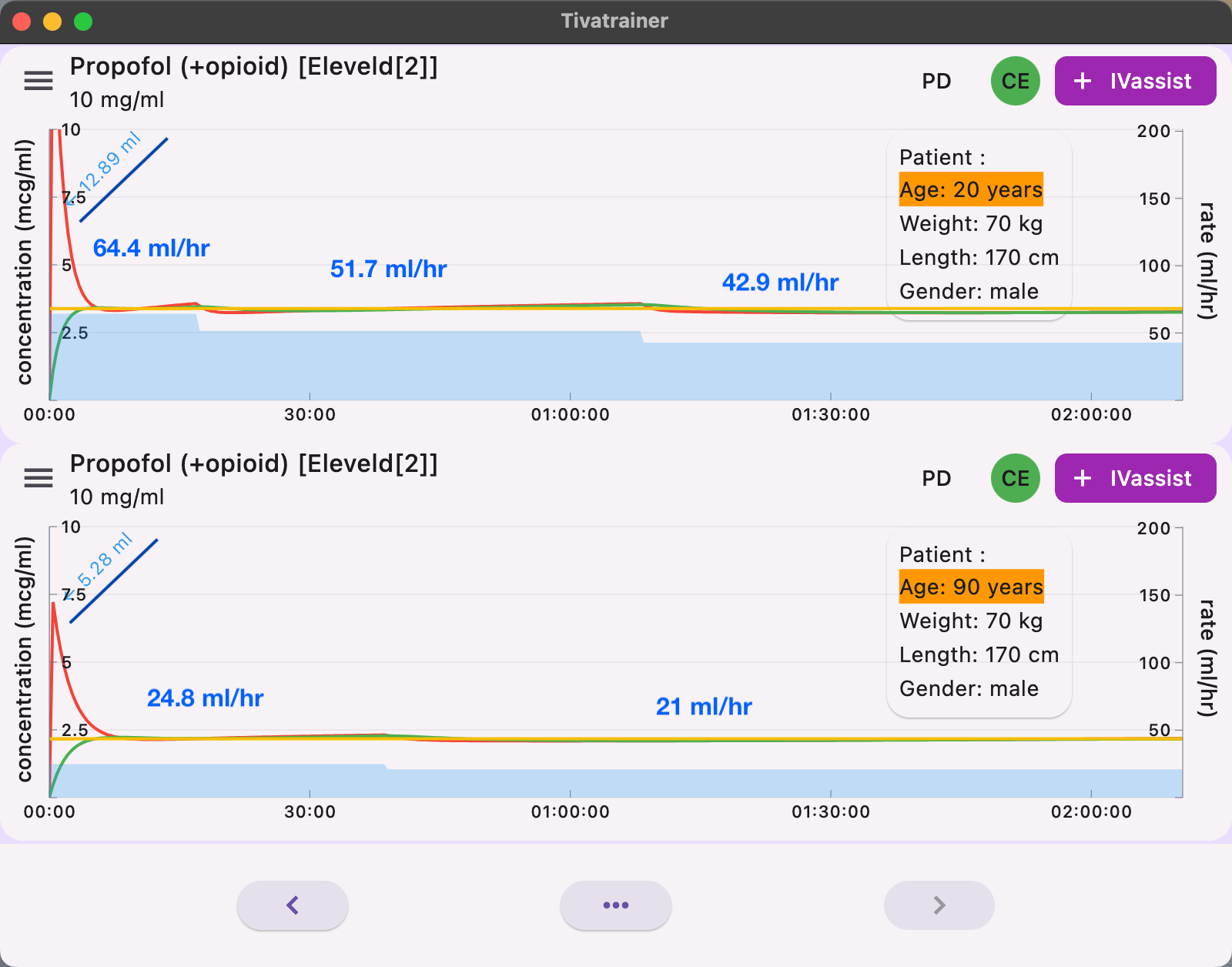
When using IVassist in Tivatrainer, the 20-year-old patient receives a bolus dose of 129 mg, compared to 53 mg for the 90-year-old. Three infusion rates--644 mg, 517 mg, and 429 mg–are required to keep the concentration within 95% of the target Ce50 of 3.4 mcg/ml for the 20-year-old. In contrast, the 90-year-old needs only two infusions--248 mg and 210 mg–to maintain a Ce50 of 2.2 mcg/ml for 2 hours of anesthesia.

You may notice that the induction bolus in IVassist is smaller than when using Effect-TCI: 129 mg versus 161 mg for the 20-year-old, and 52.8 mg versus 70 mg for the 90-year-old. The reason is simple: IVassist does not simulate stopping the infusion, as this would be error-prone if the user forgets to restart it. As mentioned earlier, not stopping the infusion could provide better predictability when the patient's pharmacokinetics deviate significantly from those programmed in the TCI device. 

How to use all this information in daily practice.

If you aim for the Ce50 in the Eleveld model that correlates with a BIS of 47, you know that 50% of your patients will have a lower BIS, and 50% will have a higher one. So, you may accept the possibility of overshoot in young, healthy patients to gain speed of induction, but in frail elderly patients, it is better to aim for the Ce50 for LOC, which is 30% less than the Ce50 in the Eleveld model. The solution is to always titrate and take your time. Start with what Gavin Kenny (THE TCI expert) has called "instant premedication". Begin with a low sedation target, for example, 1 mcg/ml, when the patient enters the OR (with no other drug!). The patient will relax, adrenaline levels will decrease, and you will get an opportunity to assess the patient's sensitivity to estimate what will be needed for adequate anesthesia. 

Blood or effect control 

In blood control, the initial dose given by the TCI device is to bring the central compartment (V1) concentration immediately to the desired target and keep it there. Only the size of the central compartment influences this loading dose. The V1 in the Marsh model is large, about 16 liters for a 70 kg patient. So the initial dose for 3 mcg/ml is 3x 16,000 = 48,000 mcg = 48 mg. In the Eleveld model, like the Schnider model, the central compartment size is relatively small: 6.3 liters, and the corresponding loading dose is about 19 mg. 

So if you start the Eleveld in blood control, you will have to wait a long time for the effect to occur unless, of course, you select an initial higher target for a period of time, guided by some guesswork.

In effect control, the pump runs and delivers just the right amount of drug so that, after stopping the pump, the increase in effect-site concentration equals the blood concentration, which is decreasing due to elimination and distribution. This equilibrium point is dependent on all the pharmacokinetic parameters. Generally, the faster the elimination and distribution, and the smaller the keo (longer thalfkeo), the higher the overshoot and the larger the induction dose. 

The keo in the Eleveld model is even smaller (longer thalfkeo) than in the Marsh model. Comparison between Marsh effect-site and Eleveld effect-site is useless in practice as there is no effect-site control mode for the Marsh model apart from the 'Modified' implementation. Although the Eleveld model decreases doses dramatically for older patients, there is no 'frailty' parameter. As explained above, if careful dosing is required, titrate in small steps toward the final target.

We present 4 clinical considerations for tightly controlled induction:

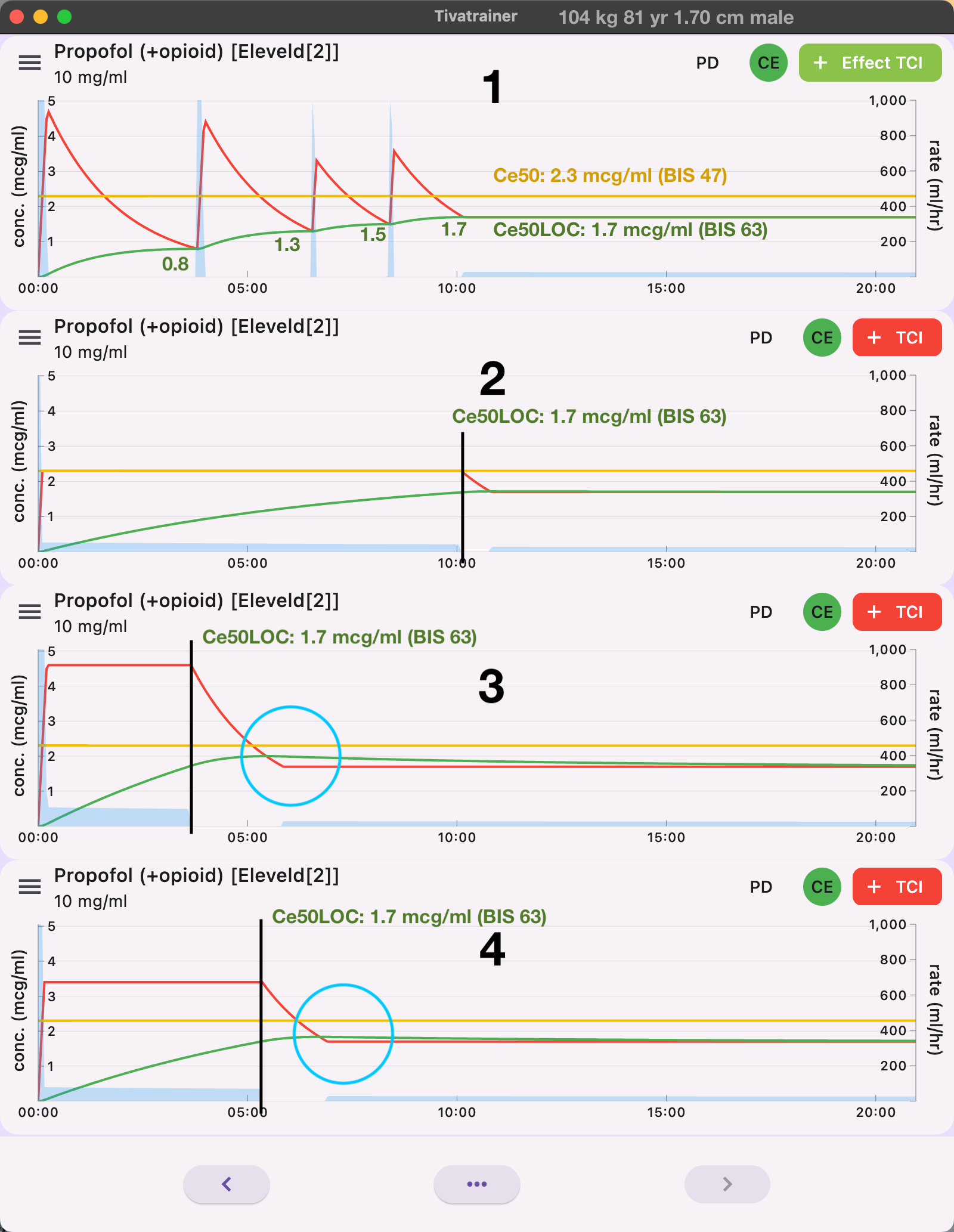
Fig 5 shows 4 approaches for a smooth induction with the Eleveld model:

1: Effect-site control using small steps, waiting for equilibrium before the next step is employed. Advantage: This method allows for the possibility of 'instant premedication' providing a quick response. Disadvantage: The result is dependent on the steps taken. For example, if the last step is 0.3 mcg/ml but only 0.1 mcg/ml is required, there will be an overshoot of 0.2 mcg/ml.
2: Blood control with target EC50. Advantage: Very little overshoot, but it results in a long induction time. Disadvantage: The control mode on the TCI device cannot be changed, so there is little effect on "instant premedication" settings, and no effect-site control is available during maintenance.
3:Blood control with initial target 2x the Cp50. The effect is observed, and the next target is set to the observed achieved effect, in this case, the CeLOC of 1.7 mcg/ml. However, despite stopping the pump, there is still a period where the concentration gradient between blood and effect exists, causing the effect to overshoot about 18%. This may not seem significant, but the dose-response curve is very steep around the point of loss of consciousness for propofol. Advantage: shorter induction time.
4: Blood control with an initial target of 2x CeLOC. CeLOC for this patient is identified using the Tivatrainer as explained in this video.

Assuming the CeLOC is at a bis of about 63, the Ce50(adequate anaesthesia) from the Eleveld model can also be used, minus 30%. Disadvantage: similar to method 2, no effect-site control is available for other stages of anesthesia. However, this approach provides minimal overshoot and a reasonable induction time.

What is the next feature to be implemented in Tivatrainer? Please send a message with your comments on these blogs to tivatrainer@gutta.tech

References:

1. Eleveld, D. J., Colin, P., Absalom, A. R. & Struys, M. M. R. F. Pharmacokinetic–pharmacodynamic model for propofol for broad application in anaesthesia and sedation. Br. J. Anaesth. 120, 942–959 (2018).
2. White, M. et al. Effect-site modelling of propofol using auditory evoked potentials. Br J Anaesth 82, 333–339 (1999).
3. Coppens, M. & Limmen, J. V. Study of the time course of the clinical effect of propofol compared with the time course of the predicted effect-site concentration: performance of three …. British journal of … (2010) doi:10.1093/bja/aeq028.
4. Zhang, M. Z., Yu, Q., Huang, Y. L., Wang, S. J. & Wang, X. R. A comparison between bispectral index analysis and auditory‐evoked potentials for monitoring the time to peak effect to calculate the plasma effect site equilibration rate constant of propofol. Eur. J. Anaesthesiol. 24, 876–881 (2007).
5. Irwin, M. G., Hui, T. W. C., Milne, S. E. & Kenny, G. N. C. Propofol effective concentration 50 and its relationship to bispectral index. Anaesthesia 57, 242–248 (2002).
6. Glen, J. B. & Engbers, F. H. M. The influence of target concentration, equilibration rate constant (ke0 ) and pharmacokinetic model on the initial propofol dose delivered in effect-site target-controlled infusion. Anaesthesia 71, 306–314 (2016).
7. Thomson, A. J., Nimmo, A. F., Engbers, F. H. M. & Glen, J. B. A novel technique to determine an ’apparent ke0 ’ value for use with the Marsh pharmacokinetic model for propofol. Anaesthesia 69, 420–428 (2014).
8. Lim, T. A. A novel method of deriving the effect compartment equilibrium rate constant for propofol. Br J Anaesth 91, 730–732 (2003).